寻找重复数-快慢指针解法原理

是龟兔赛跑。

前言

突然刷到了一个视频If Programming Was An Anime

里面的快慢指针很有趣，刚好有兴趣，那就写一下吧。

正文

要用快慢指针解决寻找重复数的话要证明两个部分。一个部分是这个题一定会构造出一个环，一个是快慢指针用来寻找环的入口的证明。

证明根据题意一定会构造出一个环

我们可以先想象出一个由1到n+1的数列，将它们打乱放置在下标从0到n的数组nums[]中。假设有个函数可以根据值返回它在数组中的下标 getIndex()

我们可以知道nums[0]的入度为0，而值为n+1的nums[getIndex(n+1)]的出度为0，数组中的其他的入度和出度都是1。这个时候可能会生成很多的环，但是如果将nums[0]作为入口的话，是不可能出现环的，因为nums[0]的入度为0，没有指向nums[0]的值。

现在我们将由nums[0]为起点的这个链表找到，假设值为n+1的数字在这个链表中，那么把它改为1~n中的任意一个数，记为p，此时我们可以知道nums[p]的入度为2，因为有两个指向它的指针。同时原本值为n+1的这个数的有了出边，指向了nums[p]

当值为p的nums[getIndex(p)]在以nums[0]开头的这个链表中时，我们可以很轻易的想象出来这个这条链表形成了一个环，包括了nums[p]到nums[x]的这一系列节点。

那么当这个值为p的nums[getIndex(p)]不在以nums[0]开头的这个链表中时，它在另外的一个链表中。举个例子[1,4,3,2,5]。此时nums[2]和nums[3]形成了一个环，我们将nums[4]的值改为3,即 nums == [1,4,3,2,3] 我们可以看到从nums[0]开始的链表最后还是会进入到一个环中。

那么值为n+1的数字不在这个链表中呢？其实这并不可能，因为它没有出边，那么它不可能在一个环中，因为所有的节点出度都是1，所以必然不存在一个环中的节点既能指向环中的节点，又能指向环外的节点。因此这个nums[getIndex(n+1)]必然在以nums[0]开头的链表中。

证明使用快慢指针来寻找环的入口

通过上面的证明我们知道了根据题意我们会构造出一个环，而环的入口就是那个重复的数。

那么我们应该怎么找到这个重复的数呢？简单地说定义两个指针，一个慢指针(slow)每次走一步，一个快指针(fast)每次走两步。当快慢指针指向的数组下标相等时就将快指针放回数组的头部，然后继续走，当快慢指针指向的数组下标相等时，这个值就是要找的环的入口。

那么问题是，怎么证明呢？

如下图，令A点为起始点，B点为环的入口，C点为慢指针首次到达B点时快指针的位置，D点为快慢指针首次在环中相遇的地点。记AB的距离为a，BC的距离为b,环的周长为R。

我们让慢指针的速度为 $v_{1}$ ，快指针的速度为 $v_{2}$ 。令$v_{2} = 2 * v_{1}$，即慢指针每次走一步，快指针每次走两步

那么当慢指针到达B点时，快指针已经走了 $S_{1} = a+b+n*R$ 其中 n 为快指针在环里已经绕过的圈数。又知道快指针的速度为慢指针的两倍，所以快指针走过的路程 $S_{1} = 2 * a$ 即慢指针走过的路程的两倍。我们将其整理可以得到 $a = n * R + b$

因为快指针每次走两步，慢指针每次走一步。所以快指针每次比慢指针多走一步。在慢指针到达B点时，快指针和慢指针的距离是 $S_{2} = S_{cb} = R - b$ 。也就是说从现在开始，到两者首次相遇在D点，慢指针要走 $S_{3} = S_{2} = R-b$ 这么多步。那么这个时候因为 $v_{2} = 2 * v_{1}$ 所以快指针走的距离为 $S_{4} = 2 * S_{2} = 2 * (R - b)$。

因为在慢指针刚到达B点时，快指针在C点，所以当两者在D点相遇时，快指针相对于B点的距离为 $S_{5} = S_{4} + b = 2 * R - b$ 。因为R为环的周长所以可以约去，因此此时快指针相对于B点的距离为 $|-b| = b$ 即D点与C点刚好形成一个对称关系。

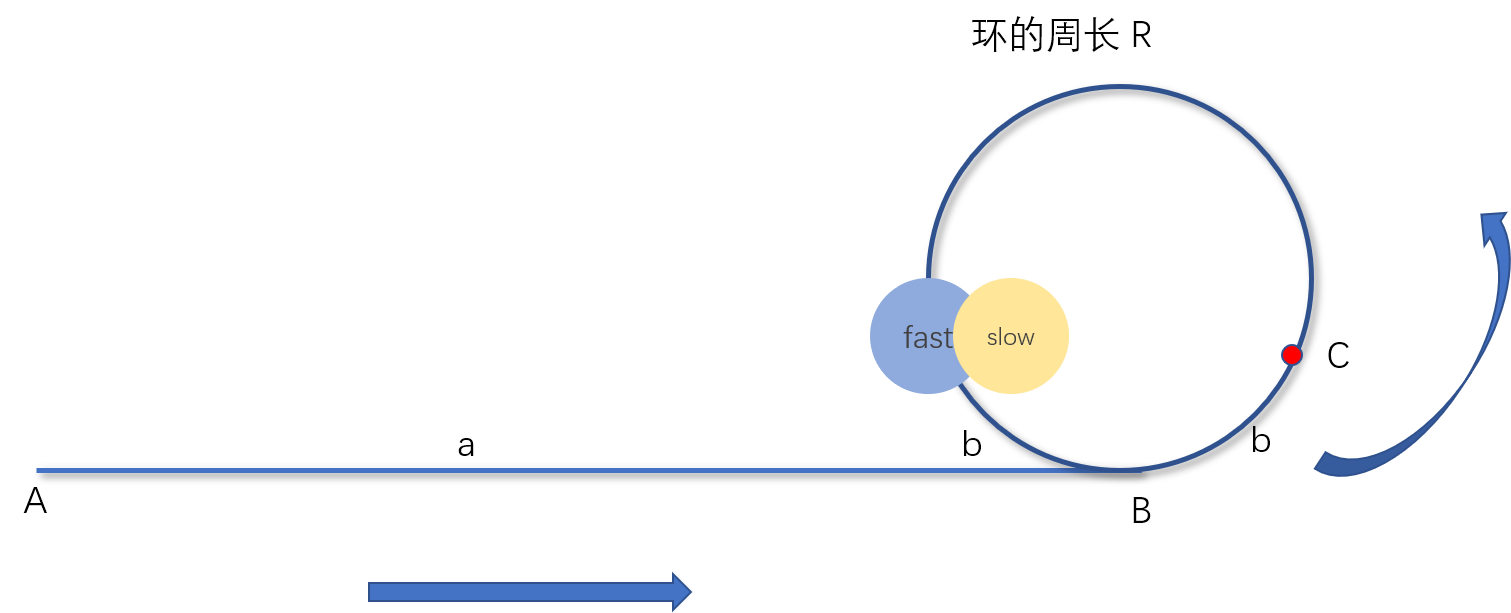
此时我们将快指针移回原点A，并且让它的速度为 $v_{3} = v_{1}$ 如果让快指针从A点走到B点那么可以知道此时快慢指针走过的路程相同 $S_{6} = a = n * R + b$ 。因为R为环的周长所以对于在环里的慢指针而言可以约去，此时我们会发现当快指针到达B点的时候，慢指针也到达了B点，此时的B点正好是环的入口。

参考

【链表】【证明】快慢指针判断链表有环、寻找环入口、计算环大小的原理